3Dの覚え書き(応用)

1. はじめに
2. 3次元空間での形状の表現
3. 画面への投影
4. 画面から3D空間への変換
5. 3D空間上での判定
6. その他
7. 履歴

1 はじめに

3D空間であれこれしたときの個人的な覚え書きです。本ページでは具体的にあれこれする場合の具体的な方法やら考え方を記しています。

2 3次元空間での形状の表現

3次元空間内の形状の表現について記す。

2.1 点の集まり

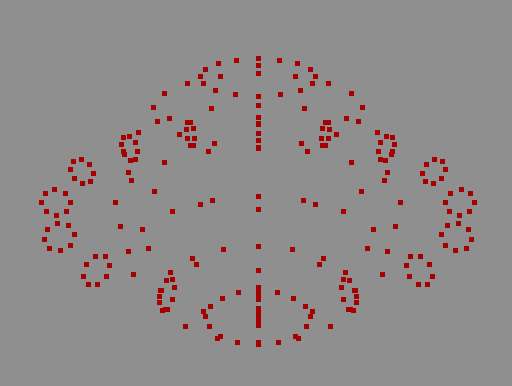
形状の外形を点の集まりと考える。形状が完全に把握できるようになるには相当量の点が必要と言える。

2.2 ワイヤーフレーム

形状の外形に沿った点同士を線で繋ぐ事で、形状が把握しやすくなる。

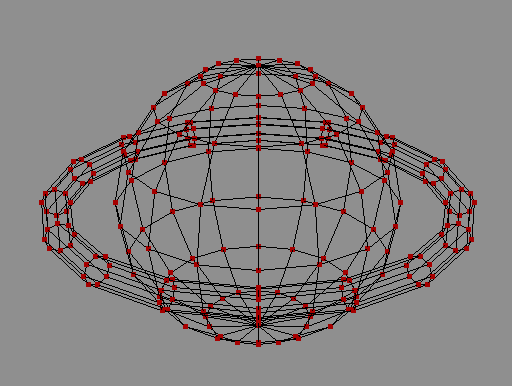
厳密に言うと線も点の集まりであると言えるのだが、線は3次元空間上で引くのではなく、2次元に投影した点同士の間に引く。ディスプレイ表示上の点の最小単位は Pixelである為、有限な点の量で表示できる。

2.3 ポリゴン

形状の外形に沿った点を 3点以上使った面として塗る事で、点の集まりやワイヤーフレームよりも形状が把握できるようになる。

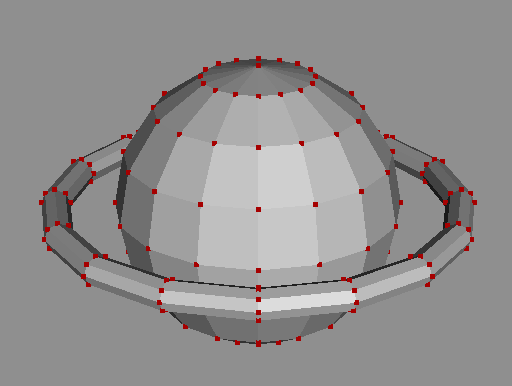
厳密に言うと面も点の集まりであると言えるのだが、ワイヤーフレームでの線と同様に面は3次元空間で塗るのではなく、2次元に投影した面で塗る。ただし面で塗る場合は、奥にある面と手前にある面を考慮して塗る必要があったり、光の当たり方を考慮して陰影を付けるように塗るなど、描画に工夫が必要となる。

2.4 式による形状表現

例えば半径がrの球の中心Pを3次元座標 (x,y,z) に置いたとき、Pからの距離が sqrt(r^2 + r^2 + r^2) 上の点Q は球の表面上の点となる。複雑な形状同士の衝突判定を球同士の衝突に置き換えて簡単化するような利用が考えられる。

3 画面への投影

3次元空間内の形状を2Dの画面に表示するときに要する座標変換について記す。

3.1 投影の要素

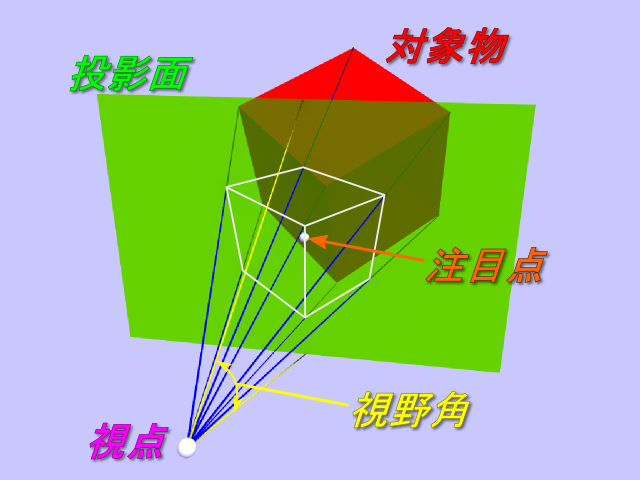
投影に必要な要素は以下が挙げられる。

視点
対象物を見る時の位置。
注目点
「視点」から見ている点。視点から注目点へのベクトルは「視線」の向きとなる。
投影面
「注目点」が乗り「視線の向き」に垂直な平面。投影面と2Dの画面が対応する。
視野角
「投影面」の大きさを決定するのに使用する。
対象物
投影面に描画する元となる3次元空間上の物体。

3.2 投影の手順

箱をガラス越しに見たとき、ガラスに箱の絵を描く例で投影の手順を示す。

首を固定する。つまり視点を決定する。
ガラスを目の前に置く。つまり投影面を用意する。
首を固定したまま(片目で見て)、箱の頂点をガラスの上にプロットする。
あとは箱を見なくても、箱の縁(辺)を描くように点を直線で結べば箱の絵が描ける。

1〜3までで箱を描くのに必要な頂点を3Dから2D(ガラス面/投影面)に座標変換していると言える。 4はどの点同士を結べば良いかが判っていれば箱を見なくても描ける。更に箱の面を塗る場合でも、箱を見なくても着色はできる。

3.3 投影に必要な計算

投影に必要な計算について記す。

3.3.1 視線ベクトルを求める

視点(eye)から対象物の頂点(P)へのベクトルを視線ベクトル(ray)は次の様に求める。視線ベクトルは正規化する。

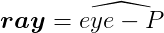
$\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle \Vec{ray} = \widehat{eye - P} $ } \end{eqnarray*}$

3.3.2 投影面の法線ベクトルを求める。

視点(eye)と注目点(center) 投影面の法線ベクトルfnを求める。法線ベクトルは正規化する。

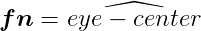
$\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle \Vec{fn} = \widehat{eye - center} $ } \end{eqnarray*}$

3.3.3 投影面と視線との交点を求める

fpを投影面上のある点(注目点を使用するのが簡単)、fnを投影面の法線ベクトル、視点をeye、視線ベクトルをrayとしたとき、交点 Pxは次の式で求める。

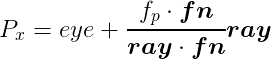
$\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle P_x = eye + \cfrac{ f_{p} \cdot \Vec{fn} }{ \Vec{ray} \cdot \Vec{fn} } \Vec{ray} $ } \end{eqnarray*}$

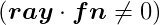
$\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle \left( \Vec{ray} \cdot \Vec{fn} \ne 0 \right) $ } \end{eqnarray*}$

rayとfnの内積が0の時は、投影面と視線ベクトルが平行となるため交点は存在しない。この場合は交点無しとして特別な処理を必要とする。

3.3.4 3D空間上の投影面座標を2D投影座標に変換する

視点と注目点が3D空間上の自由な位置にあるとしたとき、投影面上の座標は 3D座標から注目点を中心とした2D投影座標に変換する必要がある。以下に変換手順のイメージを示す。

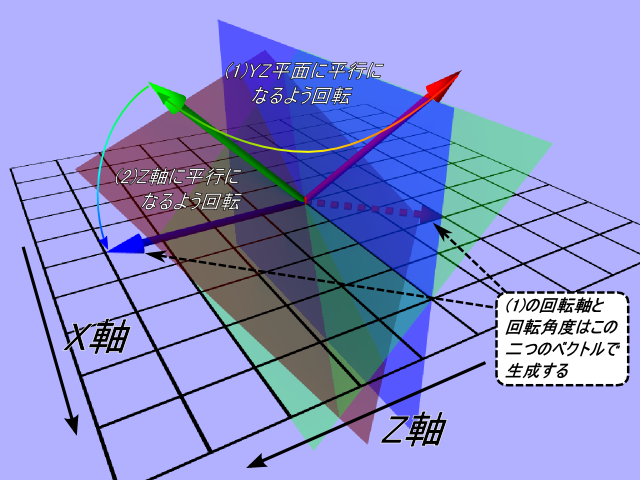
投影面法線ベクトルをYZ平面に平行になるよう回転する
投影面の法線ベクトル(N)は視点と注目点から求められる(赤の実線矢印)。 Z軸に平行なベクトルaxisZを(0.0, 0.0, 1.0)とする(青の実線矢印)。 YZ平面への回転角度と回転軸ベクトルは、「ベクトルaxisZ」と「投影面の法線ベクトルのYを0にしたベクトル(Nxz)(赤の破線矢印)」から求める。

回転角度θ1は前述二ベクトルの内積を利用して求める。

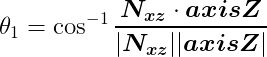
$\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle \theta_{1} = \cos^{-1} \frac{ \Vec{N_{xz}} \cdot \Vec{axisZ} }{|\Vec{N_{xz}}||\Vec{axisZ}| } $ } \end{eqnarray*}$

回転軸ベクトルvR1は二ベクトルの外積を利用して求める。vR1は単位ベクトル化する。

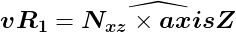
$\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle \Vec{vR_1} = \widehat{ \Vec{N_{xz}} \times \Vec{axisZ} } $ } \end{eqnarray*}$

回転角度θ1と回転軸ベクトルvR1から回転行列 R1 を求め、法線ベクトルN を回転させた法線ベクトルN1(緑の実線矢印)を求める。
Z軸に平行になるように回転する
Z軸に平行なベクトル axisZ と 1.で求めた「法線ベクトルN1」から回転角度と回転軸ベクトルを求める。

回転角度θ2は前述二ベクトルの内積を利用して求める。

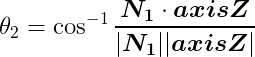
$\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle \theta_{2} = \cos^{-1} \frac{ \Vec{N_{1}} \cdot \Vec{axisZ} }{|\Vec{N_{1}}||\Vec{axisZ}| } $ } \end{eqnarray*}$

回転軸ベクトルvR2は二ベクトルの外積を利用して求める。vR2は単位ベクトル化する。

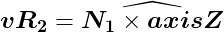
$\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle \Vec{vR_2} = \widehat{ \Vec{N_{1}} \times \Vec{axisZ} } $ } \end{eqnarray*}$

回転角度θ2と回転軸ベクトルvR2から回転行列 R2 を求める。
二つの回転を合成する
回転行列R1と回転行列R2を掛けて回転行列R3を求める。

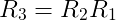
$\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle R_{3} = R_{2} R_{1} $ } \end{eqnarray*}$

R3はR1とR2の二つの回転行列を合成した回転行列となる。掛ける順番(R1R2ではない)に注意する。

回転行列R3を使って3D空間の投影面上の点を2DのXY平面座標に変換できる。投影面上にプロットした点は、注目点を中心として回転させなくてはならない。

一回で axisZに向かう回転を行うと、回転前の投影面の法線が axisZの向きと反対側に向いている場合に画面全体が回転してしまう。これは視点と注目点だけでは上下方向の情報が無い為、天地がひっくり返るような回転になってしまう。一度YZ平面上に垂直に立てることで画面全体が回転するのを防いでいる。

今回示した方法では、法線ベクトルNがY軸に平行なとき、法線ベクトルN1はゼロベクトルとなる。この場合は「1.」の回転行列はR1は単位行列(すなわち無回転行列)にする。

また、「1.」の操作で得られた法線ベクトルN1が axisZの向きと180°反対に向いているとき、「2.」で得られる回転軸ベクトルがゼロベクトルとなる。この場合は例外的に回転軸をY軸にする対処が必要になる。

3.3.5 2D投影座標をスクリーン座標に変換する

2D投影座標をスクリーン座標に変換するイメージを以下に示す。

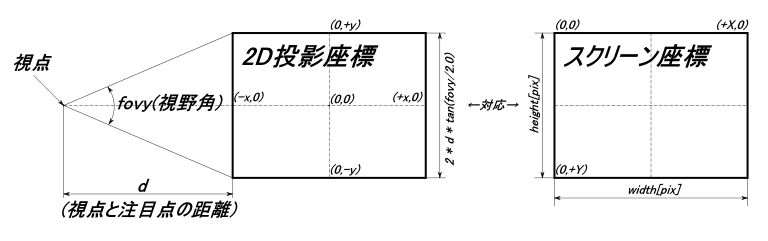
視点と注目点の距離と視野角(fovy)から2D投影座標上の範囲を決定する。2D投影座標(x,y)をクスリーン座標(X,Y)に変換する式を以下に示す。

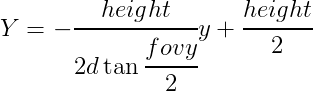
$\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle Y = - \cfrac{height}{2d \tan \cfrac{fovy}{2}} y + \cfrac{height}{2} $ } \end{eqnarray*}$

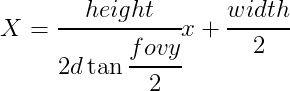
$\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle X = \cfrac{height}{2d \tan \cfrac{fovy}{2}} x + \cfrac{width}{2} $ } \end{eqnarray*}$

2D投影座標系ではy値は図の上がプラスとなるがスクリーン座標系では下がプラスとなる点を変換式に含む。また、スクリーン座標系の原点(0,0)は左上の為、スクリーンの幅と高さ (width, height)でバイアスをかける必要がある。

3.3.6 その他投影時に考慮が必要な点

いくつかの例外的な要素は投影対象としない方が良い場合がある。

視点の後ろの点は投影の必要が無い
投影手順を全ての点に適用すると、視点の後ろにある点(視野に入らない)も座標変換できてしまう。これらの点は「3.3.3」前に除外するのが効率が良いと考えられる。
遠くにある点を投影対象から省く
遠くにある物体は描画自体を行わなくても良い場合がある。視点から距離により、描画対象にするかしないかを判断する方法が考えられる。

4 画面から3D空間への変換

マウスのカーソル位置(スクリーン座標)から3D空間座標への変換について記す。

「3」で示した手順を逆の順で変換する。変換の結果得られる点の位置は3D空間上の投影面上になる。

5 3D空間上での判定

3D空間上での各種判定とその方法について記す。

5.1 直線と点との距離

マウスである形状の頂点を選択する場合、視点からマウスカーソル位置を3D空間に変換した点への視線上もしくは視線に近い点を選択対象とする方法が考えられる。これは線と点の距離で求められる。以下に線と点との距離の求め方を示す。

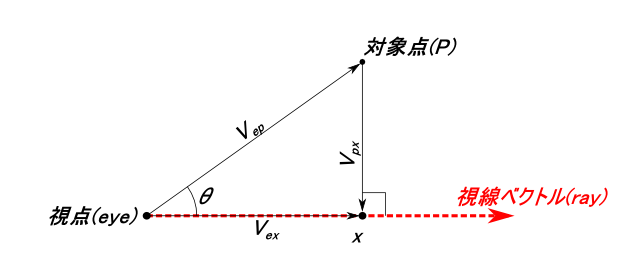
図のVpxの長さが点Pと線rayの最短距離となる。以下の式で求める。

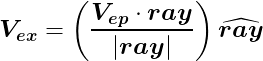
$\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle \Vec{V_{ex}} = \left( \frac{\Vec{V_{ep}} \cdot \Vec{ray}}{|\Vec{ray}|} \right) \widehat{\Vec{ray}} $ } \end{eqnarray*}$

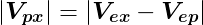
$\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle |\Vec{V_{px}}| = |\Vec{V_{ex}} - \Vec{V_{ep}}| $ } \end{eqnarray*}$

視線からの距離が近いものを選ぶ場合は、各点の Vexの長さを比較して最も短いものを選べば良い。

5.2 面と点との距離

無限平面と点との距離の求め方を示す。

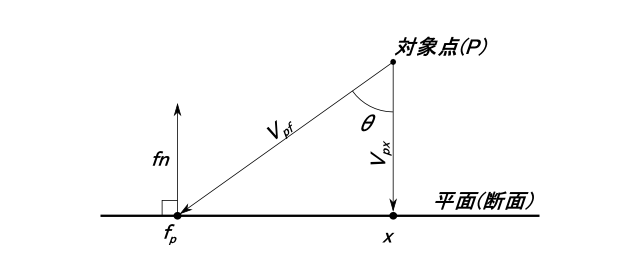
fpを平面上の任意の点、fnを平面の法線ベクトル(単位ベクトル)、Pを対象点、 Pから面への最短ベクトルをVpxとしたとき、Vpxの長さが面と点Pとの距離となる。

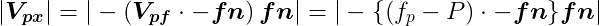
$\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle |\Vec{V_{px}}| = | - \left( \Vec{V_{pf}} \cdot -\Vec{fn} \right) \Vec{fn} | = | - \{ \left( f_p - P \right) \cdot - \Vec{fn} \} \Vec{fn} | $ } \end{eqnarray*}$

5.3 直線と面の交点

「3.3.3」で使用した式を利用する。

5.4 線分上の点の判定

「5.1」などで求めた直線上の点が、同直線のある線分内に収まっているかを判断する方法を示す。

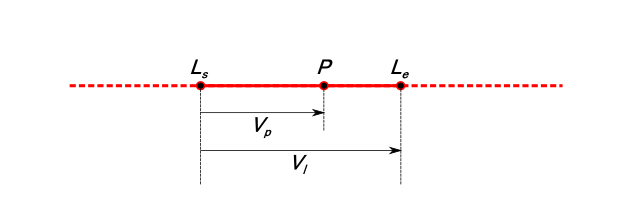
線分の始点をLs、終点をLeとたとき、LsからLeに向かう線分ベクトルをVl、線分の始点Lsから点Pに向かうベクトルをベクトルVp とする。これらを使用して以下の式求められるxを使用して判定する。

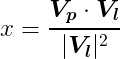
$\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle x = \cfrac{ \Vec{V_{p}} \cdot \Vec{V_{l}} }{ | \Vec{V_{l}} | ^{2} } $ } \end{eqnarray*}$

xが0より小さい場合もしくは1より大きい場合は線分内に収まっていない。

この式では、点Pは線分の直線に乗っている必要は無い。直線に乗っていない場合は直線に最も近い点で判断している事になる。

5.5 多角形内の点の判定

点が多角形(ポリゴン)内にあるか否かを判定する方法を示す。点は多角形と同一平面上にあるものとする。

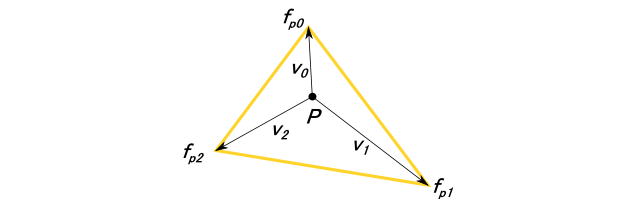
図の三角形の各頂点をfp0,fp1,fp2、点Pから各頂点に向かうベクトルをv0,v1,v2とする。このとき、v0とv1の外積、v1とv2の外積、v2とv0の外積で得られるベクトルが全て同じ向きであれば、三角形fp0,fp1,fp2の内側に点Pはあると判断できる。向きの判定には内積を使用する。

この方法は凸ポリゴン(全ての頂点の内角が180°以下である多角形)であれば、四角形以上の場合でも適用できる。凹ポリゴン(頂点に180°より大きい内角を含む多角形)の場合はこの方法では判断できない。

点Pが多角形の辺または頂点と同じ座標の場合、途中で得られる外積ベクトルがゼロベクトルになる。辺や頂点も内側に含む場合は、面の法線ベクトルを基準にして判定するなどの工夫が必要になる。

6 その他

自分用によく使う分だけメモっとくくらいのつもりで作成しました。そんな訳であまり参考にならないかも知れませんが、もし役に立つことがあれば幸いです。

本ページは以下のフリーソフトで作成しました。

Emacsの org-modeを使って作成しました。
画像は Wingw3D、POV-ray、Inkscape、GIMP を使用して作成しました。
数式は Cygwinパッケージの TeX Live を使用してorg-modeでHTMLエクスポート時にインライン画像変換しています。

7 履歴

  2012/04/28 : 初版。
  2013/03/17 : 数式をorg-modeを使ってインライン画像変換で生成するようにした。
  2013/03/31 : TOP、PREVのリンクを間違えていたのを修正。本文に変更はありません。
  2013/06/16 : org-mode 8.0.x対応。
  2014/11/08 : orgソース記述見直し。本文の内容に変更ありません。

TOP PREV