3Dの覚え書き(基礎)

Table of Contents

1 はじめに

3D空間であれこれ計算する個人的な覚え書きです。本ページでは基本的な計算式について 記しています。ベクトルや行列は一般式があるかと思いますが、ここでは3Dに特化した表現で 記しています。

2 位置とベクトル

3次元の直行座標系を用いる。3次元座標系の中で表現する位置やベクトルについて示す。

2.1 3次元位置

位置の表現は P(x,y,z)で示す。プログラム上では構造体やクラスを使用して表現するのが 色々と具合が良い。以下、構造体で表現した例を示す。 

struct Point{
   double x ;
   double y ;
   double z ;
}

2.2 3次元ベクトル

大きさと向きを持った量を示す。ある点Aからある点Bに向かうベクトルvは

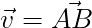
\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle \vec{v}=\vec{AB} $ } \end{eqnarray*}

と表現される。プログラム上では 点の構造体を使用するとベクトルvは、 

v.x = A.x - B.x ;
v.y = A.y - B.y ;
v.z = A.z - B.z ;

のような感じで求める。

2.3 3次元ベクトル演算

3次元ベクトルの演算について記す。

2.3.1 ベクトル同士の加減算

ベクトルaとベクトルbの和cおよび差dは以下のように求められる。

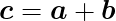
\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle \Vec{c}=\Vec{a} + \Vec{b} $ } \end{eqnarray*}

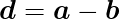
\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle \Vec{d}=\Vec{a} - \Vec{b} $ } \end{eqnarray*}

プログラム上では、 

// 和
c.x = a.x + b.x ;
c.y = a.y + b.y ;
c.z = a.z + b.z ;
// 差
d.x = a.x - b.x ;
d.y = a.y - b.y ;
d.z = a.z - b.z ;

のような感じで求める。

2.3.2 ベクトルのスカラー倍

ベクトルaの長さをN倍する場合は以下のように求められる。

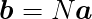
\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle \Vec{b}=N \Vec{a} $ } \end{eqnarray*}

プログラム上では、 

// スカラー倍
b.x = a.x * N ;
b.y = a.y * N ;
b.z = a.z * N ;

のような感じで求める。Nがマイナスの場合、ベクトルの向きが逆になると言える。

2.3.3 ベクトルの大きさ(長さ)

ベクトルvの大きさ(長さ)は以下のように求められる。

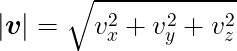
\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle |\Vec{v}| = \sqrt{ v_{x}^{2} + v_{y}^{2} + v_{z}^{2} } $ } \end{eqnarray*}

プログラム上では式のまま、 

v_leng = sqrt( v.x*v.x + v.y*v.y + v.z*v.z ) ;

のような感じで求める。

2.3.4 単位ベクトル

ベクトルの大きさ(長さ)が 1.0 のベクトルを単位ベクトルと呼ぶ。ベクトルvの単位ベクトルは次の様に求められる。

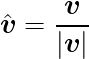
\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle \hat{\Vec{v}}=\frac{\Vec{v}}{|\Vec{v}|} $ } \end{eqnarray*}

単位ベクトルにする事を正規化(normalize)するとも言う。

プログラム上では、 

v_leng = sqrt( v.x*v.x + v.y*v.y + v.z*v.z ) ;
if( v_leng!=0.0 ){
  vn.x = v.x/v_leng ;
  vn.y = v.y/v_leng ;
  vn.z = v.z/v_leng ;
}else{
  vn.x=0.0 ;
  vn.y=0.0 ;
  vn.z=0.0 ;
}

のような感じで求める。ベクトルvの大きさが 0.0の場合に具合が悪いので、 都合の良い方法で対処する必要がある。例では「ゼロベクトル」としています。

2.3.5 ベクトルの内積

ベクトルaとベクトルbの内積 d は以下の式で求められる。

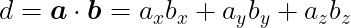
\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle d = \Vec{a} \cdot \Vec{b} = a_x b_x + a_y b_y + a_z b_z $ } \end{eqnarray*}

プログラム上では式の通り、 

d = a.x*b.x + a.y*b.y + a.z*b.z ;

のような感じで求める。求まる値dはスカラー量である。 内積は以下の等式が成立する。

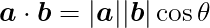
\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle \Vec{a} \cdot \Vec{b} = |\Vec{a}||\Vec{b}| \cos \theta $ } \end{eqnarray*}

θはベクトルaとベクトルbのなす角である。

2.3.6 ベクトルの外積

ベクトルaとベクトルbの外積で求められるベクトル c は以下の式で求められる。

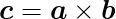
\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle \Vec{c} = \Vec{a} \times \Vec{b} $ } \end{eqnarray*}

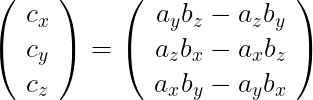
\begin{eqnarray*} \mbox{\Large $ \displaystyle \left( \begin{array}{c} c_x \\ c_y \\ c_z \end{array} \right) = \left( \begin{array}{c} a_y b_z - a_z b_y \\ a_z b_x - a_x b_z \\ a_x b_y - a_y b_x \end{array} \right) $ } \end{eqnarray*}

プログラム上では式の通り、 

c.x = a.y*b.z - a.z*b.y ;
c.y = a.z*b.x - a.x*b.z ;
c.z = a.x*b.y - a.y*b.x ;

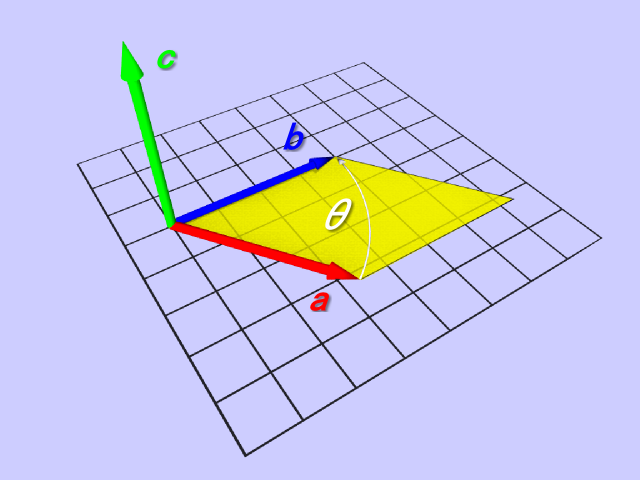
のような感じで求める。外積で求められるベクトルcは以下のようになる。

  • ベクトルaの始点とベクトルbの始点を(0.0, 0.0, 0.0)に置いた時、ベクトルaとベクトルbのなす平面 に垂直な軸に平行となる。
  • ベクトルaの始点とベクトルbの始点を(0.0, 0.0, 0.0)に置いたまま、ベクトルaの終点をベクトルbの終点 に向かうようにベクトルaを回転させる。180°以内でベクトルbに重なる方向に回した時、 ベクトルcの向きは 右ネジの方向と 同じとなる。

また、ベクトルcの大きさには以下の等式が成立する。

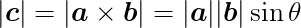
\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle | \Vec{c} | = | \Vec{a} \times \Vec{b} | = |\Vec{a}||\Vec{b}| \sin \theta $ } \end{eqnarray*}

θ はベクトルaとベクトルbのなす角である。また、ベクトルaとベクトルbで形成される 平行四辺形の面積に等しい。

cross_img.png

2.4 3次元直線

始点P1と終点P2 を結ぶ直線は、始点と始点から終点に向かう方向ベクトルで表現する場合がある。

2.5 3次元平面

同一直線上に無い 三つの点 P1, P2, P3 を面として表現する場合がある。三点の内側を 有限の面として扱うのに便利。

別の表現方法として、平面上のある点と 面に垂直な方向ベクトルで表す場合がある。 この平面は無限平面として扱う。

面に垂直な方向ベクトルは、P1からP2に向かうベクトルvaとP1からP3に向かうベクトルvbの 外積で求められる。正規化された方向ベクトルを面の法線ベクトルと呼ぶ。面の法線ベクトル の向きと視線ベクトルの向きから面の表と裏を判定する事ができる。

3 行列

行列について示す。

3.1 回転行列

回転軸ベクトルr を回転軸として 右ネジの向きにθ°回転させる回転行列Rを以下に示す。 回転軸ベクトルrは単位ベクトルに正規化しているものとする。

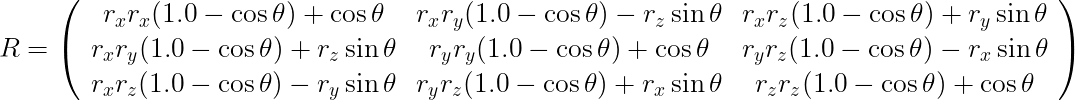
\begin{eqnarray*} \mbox{\Large $ \displaystyle R = \left( \begin{array}{ccc} r_x r_x (1.0 - \cos \theta) + \cos \theta & r_x r_y (1.0 - \cos \theta) - r_z \sin \theta & r_x r_z (1.0 - \cos \theta ) + r_y \sin \theta \\ r_x r_y (1.0 - \cos \theta) + r_z \sin \theta & r_y r_y (1.0 - \cos \theta) + \cos \theta & r_y r_z (1.0 - \cos \theta ) - r_x \sin \theta \\ r_x r_z (1.0 - \cos \theta) - r_y \sin \theta & r_y r_z (1.0 - \cos \theta) + r_x \sin \theta & r_z r_z (1.0 - \cos \theta ) + \cos \theta \end{array} \right) $ } \end{eqnarray*}

位置Pの点を回転行列Rによって回転した位置Nの点は以下の行列演算で求める。

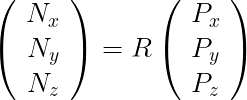
\begin{eqnarray*} \mbox{\Large $ \displaystyle \left( \begin{array}{c} N_x \\ N_y \\ N_z \end{array} \right) = R \left( \begin{array}{c} P_x \\ P_y \\ P_z \end{array} \right) $ } \end{eqnarray*}

プログラム上では次のような感じで求める。 

n.x = R[0][0]*p.x + R[0][1]*p.y + R[0][2]*p.z ;
n.y = R[1][0]*p.x + R[1][1]*p.y + R[1][2]*p.z ;
n.z = R[2][0]*p.x + R[2][1]*p.y + R[2][2]*p.z ;

3.2 回転行列の積

二つの回転行列を掛ける事で、二つの回転を合成した回転行列を生成できる。

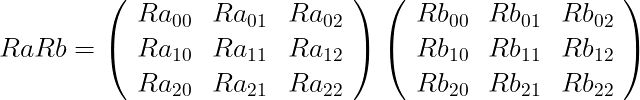
\begin{eqnarray*} \mbox{\Large $ \displaystyle Ra Rb = \left( \begin{array}{ccc} Ra_{00} & Ra_{01} & Ra_{02} \\ Ra_{10} & Ra_{11} & Ra_{12} \\ Ra_{20} & Ra_{21} & Ra_{22} \end{array} \right) \left( \begin{array}{ccc} Rb_{00} & Rb_{01} & Rb_{02} \\ Rb_{10} & Rb_{11} & Rb_{12} \\ Rb_{20} & Rb_{21} & Rb_{22} \end{array} \right) $ } \end{eqnarray*}

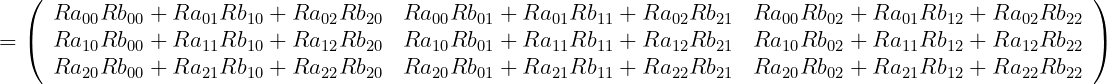
\begin{eqnarray*} \mbox{\large $ \displaystyle = \left( \begin{array}{ccc} Ra_{00}Rb_{00}+Ra_{01}Rb_{10}+Ra_{02}Rb_{20} & Ra_{00}Rb_{01}+Ra_{01}Rb_{11}+Ra_{02}Rb_{21} & Ra_{00}Rb_{02}+Ra_{01}Rb_{12}+Ra_{02}Rb_{22} \\ Ra_{10}Rb_{00}+Ra_{11}Rb_{10}+Ra_{12}Rb_{20} & Ra_{10}Rb_{01}+Ra_{11}Rb_{11}+Ra_{12}Rb_{21} & Ra_{10}Rb_{02}+Ra_{11}Rb_{12}+Ra_{12}Rb_{22} \\ Ra_{20}Rb_{00}+Ra_{21}Rb_{10}+Ra_{22}Rb_{20} & Ra_{20}Rb_{01}+Ra_{21}Rb_{11}+Ra_{22}Rb_{21} & Ra_{20}Rb_{02}+Ra_{21}Rb_{12}+Ra_{22}Rb_{22} \end{array} \right) $ } \end{eqnarray*}

回転の順番は Rb, Ra の順になる。式の並びの順と逆にしなくてはならない。

4 クォータニオン(四元数)

クォータニオンは一つの実部と3次元の虚部を併せ持つ超複素数系のひとつである。

4.1 クォータニオンの定義

クォータニオン qは次の様に定義する。

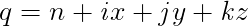
\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle \Vec{ } q = n + {\it i}x + {\it j}y + {\it k}z $ } \end{eqnarray*}

nが実部、ix,jy,kxが虚部となり、虚部は3次元空間ベクトルに対応付ける事ができる。

プログラム上では次のような感じで表現する事にする。 

struct Quaternion{
   double n  ;
   double vx ;
   double vy ;
   double vz ;
}

4.2 クォータニオンと回転

クォータニオンは回転軸と回転量を保持する値として扱う事ができる。 3次元の回転軸ベクトル v を軸として右ネジの向きにθ°回転させる クォータニオンqは以下の様に求められる。 ただし、回転軸ベクトル v は 単位ベクトルに正規化されているものとする。

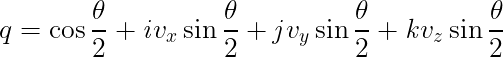
\begin{eqnarray*} \def\Vec#1{\mbox{\boldmath $#1$}} \mbox{\Large $ \displaystyle \Vec{ } q = \cos \frac{\theta}{2} + {\it i} v_x \sin \frac{\theta}{2} + {\it j} v_y \sin \frac{\theta}{2} + {\it k} v_z \sin \frac{\theta}{2} $ } \end{eqnarray*}

プログラム上では次のような感じで変換する。 

q.n  = cos( th/2.0 ) ;
q.vx = v.x * sin( th/2.0 ) ;
q.vy = v.y * sin( th/2.0 ) ;
q.vz = v.z * sin( th/2.0 ) ;

クォータニオンから回転軸ベクトルと回転角度を取り出す事もできる。 

th  = 2.0 * acos( q.n ) ; // 回転角度
v.x = q.vx ;
v.y = q.vy ;
v.z = q.vz ;
v.normalize() ;           // 回転軸ベクトル(単位ベクトル)

回転角度が0のとき、虚部がゼロベクトルになるので、都合の良いように対応する必要がある。

4.3 クォータニオンの積

二つのクォータニオンの積により、それぞれ保持している回転を合成する事ができる。 

Quaternion qa, qb, qc ;

// qc = qa * qb
qc.n  = (qa.n * qb.n ) - (qa.vx * qb.vx) - (qa.vy * qb.vy) - (qa.vz * qb.vz) ;
qc.vx = (qa.n * qb.vx) + (qa.vx * qb.n ) + (qa.vy * qb.vz) - (qa.vz * qb.vy) ;
qc.vy = (qa.n * qb.vy) + (qa.vy * qb.n ) + (qa.vz * qb.vx) - (qa.vx * qb.vz) ;
qc.vz = (qa.n * qb.vz) + (qa.vz * qb.n ) + (qa.vx * qb.vy) - (qa.vy * qb.vx) ;

4.4 クォータニオンと回転行列

クォータニオンを回転行列に変換できる。 

m[0][0] = 1 - 2*( q.vy * q.vy + q.vz * q.vz ) ;
m[0][1] =     2*( q.vx * q.vy - q.n  * q.vz ) ;
m[0][2] =     2*( q.n  * q.vy + q.vx * q.vz ) ;

m[1][0] =     2*( q.vx * q.vy + q.n  * q.vz ) ;
m[1][1] = 1 - 2*( q.vx * q.vx + q.vz * q.vz ) ;
m[1][2] =     2*( q.vy * q.vz - q.n  * q.vx ) ;

m[2][0] =     2*( q.vx * q.vz - q.n  * q.vy ) ;
m[2][1] =     2*( q.vy * q.vz + q.n  * q.vx ) ;
m[2][2] = 1 - 2*( q.vx * q.vx + q.vy * q.vy ) ;

上記で求めた回転行列を介して3次元位置Pを回転後の座標に移動する。

5 その他

自分用によく使う分だけメモっとくくらいのつもりで作成しました。 そんな訳であまり参考にならないかも知れませんが、もし役に立つことがあれば幸いです。

本ページは以下のフリーソフトで作成しました。

  • Emacsの org-modeを使って作成しました。
  • 画像は Wingw3D、POV-ray、Inkscape を使用して作成しました。
  • 数式は Cygwinパッケージの TeX Live を使用してorg-modeでHTMLエクスポート時にインライン画像変換しています。

6 履歴

  2012/04/28 : 初版。
  2013/03/17 : 数式をorg-modeを使ってインライン画像変換で生成するようにした。
  2013/03/31 : TOP、PREVのリンクを間違えていたのを修正。本文に変更はありません。
  2013/06/16 : org-mode 8.0.x対応。
  2014/11/08 : orgソース記述見直し。本文の内容に変更はありません。
  2015/02/28 : 回転行列の積の式を修正。
  2015/06/28 : 内積のプログラム例が間違えていたのを修正。
TOP PREV

Author: TANE

Emacs 24.5.1 (Org mode 8.2.10)