HSVホイールを作ったときの話
目次
1. はじめに
ペイントソフトなどで色を選択するのに、HSVホイールによる方式があります。 便利なライブラリを使えば、サクッと利用できるところなんだろうとは思いますが、 D言語でもそもそコーディングしていると自前で用意する必要があります。そんな訳で、 暇つぶしになんとなく作ろうとした訳なのですが、実際に作ってみると意外と面倒臭い事になりました。 でも、何気に色々なアルゴリズム要素を含んでいて面白かったので、使用したアルゴリズム なんかについてメモっておきたいと思います。
本ページでは説明の為に作図ソフトのCinderella で作成した インタラクティブに操作可能な図を使用しています。 ただ、2022年7月2日時点でうまく表示できない要素がある為、説明との対応が判らない場合は 元ファイル(*.cdy)をダウンロードしていただき、 Cinderella で直接開いていただく必要がある点をご容赦ください。
2. 観察してみる
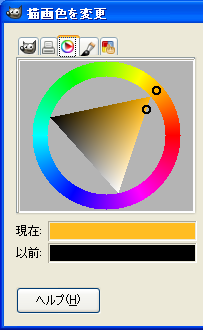
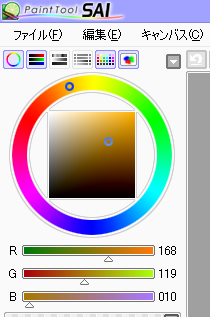
HSVホイールにはいくつか方式があるようですが、明度と彩度の指定方法で分けると二つに分類できると 思います。一つは三角形の領域で指定するもの、もう一つは四角形の領域で指定するものです。
| 三角形の例(GIMPなど) | 四角形の例(SAIなど) |
|---|---|
 |
 |
なんとなく「三角形の方式」を作ってみる事にしました。このウッカリした選択が面倒臭い事になろうとは、 針の先ほども想像していませんでした(^^; さておき、この三角形の方式では、中の三角形が色相に合わせて回転するもの(GIMPなど)と、回転しない ものに分かれるようですが、「回転するもの」を考えてみる事にしました。
3. 何があれば良い?
何があれば実装できるか少し考えてみました。
- マウスポインタ位置をHSV値に変換する。
- ウインドウサイズに従って色相サークルを描く。
- HSV値にしたがって色相サークルの内側にHSV三角形を描く。
まぁ、ザックリこんなのがあれば良いかな?マウスポインタ位置を一度HSV値に変換して、 HSV値から絵を作るとしたのは、例えばRGB値で色調節をするウインドウが別に存在したとき、 そちらで調節した色にHSVホイールを連動させる事ができると考えたからです。
4. 作ってみる
そんな訳で、早速作ってみることにしました。
4.1. 操作を判別する
まずはマウスポインタ位置をHSV値に変換する方法を考えてみます。
実は二つの指定を切り替える必要があります。一つはHSV三角形内の位置を操作しているか。 もう一つは色相サークルの位置を操作しているか。 そこで、マウスのドラッグ開始点が HSV三角形内を選択していれば三角形内位置を操作し、 三角形外を選択すれば色相サークルを操作する、という感じに考えてみました。
「HSV三角形は回転できる」事にしたので、回転した状態で三角形の内外判定を行う 必要があります。そんな訳で、ここでは以下の図(Cinderellaという作図ソフトで 作画した図です。PやHの赤い点をドラッグで動かせます)を参照しながら判定方法を考えてみます。
元ファイル:hsv_triangle2.cdy
まず、中心点Oを(0,0)とし、色相(hue)が0°の場合の三角形を想定します。 色相htは -180°〜+180°の範囲を取る事とします。 また、色相サークルは中心点をOとして、半径RIから半径ROの範囲に描くものと しています。Pはマウスのポインタ位置とします。 三角形の1点は色相(hue)に従って位置が決まります。他の2点は色相の位置に従って 位置が決まります。なので、各点の座標(x,y)は
H( RI*cos(ht ), RI*sin(ht ) ) V( RI*cos(ht+120°), RI*sin(ht+120°) ) S( RI*cos(ht-120°), RI*sin(ht-120°) )
という感じになるでしょうか。 続いて、点Pがこの三角形の内側にあるか否かを判定します。ここでは平面上のベクトルと 外積を利用しました。PからHに向かうベクトルをvecPHてな感じで表現し、外積は「×」 で表現すると、
- 「 (vecPH × vecPV) と (vecPV × vecPS) と (vecPS × vecPH)」の三つの外積の結果が全て正、もしくは全て負ならば、三角形HVSの内側に点Pが存在する。
という感じで判定できます。 「三角形の内外判定」というキーワードでWeb検索してみれば、もっと良い説明を してくれてるページがあると思います(^^; 3Dだと外積の結果はベクトルとして 扱う必要があるので、全てが同じ方向である事をもう少し厳密にチェックしなくては なりませんが、2DでXY平面上の点のみを扱ってますので、正か負かだけを見れば良い という感じで考えました。
そんな訳で、ひとまずHSV三角形を操作するのか、色相サークルを操作するのかを、 これで切り替えられる感じになりました。
4.2. 点位置から色相に変換する
色相サークルを操作する事を考えます。 点Pの位置を色相に変換する訳ですが、これは単純に以下の様にしました。
ht = acos( P.x/sqrt((P.x)^2 + (P.y)^2) ) * ((P.y<0) ? -1.0 : 1.0)
ベクトルOPがX軸に対してなす角をacos()でもって求めてるだけです。ただし、acos()の返す範囲は 0°〜180°なので、点PのY位置が正でも負でも同じ結果になります。そこで、 点PのY位置が負の場合は-1.0倍する事で、-180°〜+180°の計360°分を範囲として 変換するようにしました。
4.3. 点位置から明度/彩度に変換する
HSV三角形内を操作する事を考えます。三角形HVS内の点Pの位置から明度(V)と彩度(S)の 割合を求めます。
さて、どうするか少し迷ったのですが、三角形HVS内を三つに分割した、それぞれの三角形 の面積比で決定する事にしてみました。
Vの割合 = △PSHの面積/△HVSの面積 Sの割合 = △PHVの面積/△HVSの面積 Hの割合 = △PVSの面積/△HVSの面積 (実際にはこれは使用しない)
得られる範囲はいずれも 0.0〜1.0になります。各三角形の面積を求める必要がありますが、 ここでもベクトルの外積を利用しました。例えば△PSHの面積は
△PSHの面積 = (vecPS × vecPH)/2.0
となります。外積の大きさは二つのベクトルで形成できる平行四辺形の面積と等しい ので、三角形の面積はその半分という訳です。これと同じ要領で、△PHV, △PVS, △HVS の面積も求めれば、面積比を得られるという事になります。 これで、明度(0.0〜1.0)と彩度(0.0〜1.0)の値が得られました。
4.4. HSV値から点をプロットする
HSV値から、HSV三角形のどこら辺を選択しているのか、色相サークルのどこら辺を選択しているのかを 得ます。元々マウスカーソルからHSV値を得たのですから、マウスカーソル位置は得られているような もんなのですが、「何があれば良い?」で少し触れたように、他の色調節ウインドウやスポイトで得た 色を入力とした場合に対応する為です。
色相ht からカラーサークル上の座標に変換するのは、以下のように考えました。
H( RI*cos(ht), RI*sin(ht) )
結局これは、HSV三角形の頂点Hの座標を描くのと同じですね。ウインドウ表示上サークルの枠内に描く ならば、RIの値を少し増やしてやれば良いと思います。
続いて、明度(V)と彩度(S)から、HSV三角形内の座標を求めます。これがね、とても面倒臭かったんです(^^; 位置PからV,Sを求めるのは三角形の面積比を利用しました。今度はこの面積比から、実際の三角形を 求めるという事になります。
元ファイル:sv_cross2.cdy
P位置を求める手順を示します。
- 線分SHを三角形の底辺、高さ方向を vecV1Vとする。高さは方向だけが合っていれば良い ので、(0,0)-(1,0)のベクトルを120°回転させたもので良い。
- 高さベクトルvecV1V をV値でスケールする。このベクトルはvecV1V2になる。
- 線分SHをvecV1V2の方向に移動する。これが直線lVとなる。この直線上に乗っている点は 線分SHを底辺とすると、どこにあっても面積は同じです(すなわち答えが無限に存在する)。
- 線分HVを三角形の底辺、高さ方向を vecS1Sとする。高さは方向だけが合っていれば良い ので、(0,0)-(1,0)のベクトルを-120°回転させたもので良い。
- 高さベクトルvecS1S をS値でスケールする。このベクトルはvecS1S2になる。
- 線分HVをvecS1S2の方向に移動する。これが直線lSとなる。この直線上に乗っている点は 線分HVを底辺とすると、どこにあっても面積は同じです。
- 直線lVと直線lSの交点を求める。ここがV値とS値から求めた位置Pになります。
最後に2直線の交点を求める必要があります。求め方は色々あるようですが、 こちら のWebサイト にあった、ベクトルを用いた方法が一番良さげみたいだったので使ってみました。 まず答えとなる式は以下のような感じです。
- 点A1から点A2に向かうベクトルを線分Aとする。
- 点B1から点B2に向かうベクトルを線分Bとする。
- 「線分A×線分B」 が 0 の時は平行なので交点無し。(※「×」は外積)
- 交点P = 線分A * (線分B×vecA1B1)/(線分B×線分A) + A1
すみません、私には何故これで良いのか式だけ見ても良くわかりませんでした(^^; そこで、 式を作図してみました。
元ファイル:intersect2.cdy
線分上に交点Pがあるとします。ポイントは以下のような感じでしょうか。
- vecA1B1とvecB1B2(すなわち線分B)の外積の大きさは、「平行四辺形 A1B2'B2B1 の面積(図の薄黄色の領域)」になります。
- vecA1A2(すなわち線分A)とvecB1B2(線分B)の外積の大きさは「平行四辺形 A1B2'A2'A2の面積(図の薄緑色の領域)」になります。
- 「平行四辺形 A1B2'B2B1 の面積(図の薄黄色の領域)」と、「平行四辺形 A1B2'P'Pの面積」は同じ面積です。
- 「平行四辺形 A1B2'A2'A2の面積(図の薄緑色の領域)」と「平行四辺形 A1B2'P'Pの面積」はどちらも底辺vecA1B2' です。すると、交点Pに相当する位置は vecA1A2(線分A)を 前述並行四辺形の面積比倍すると、vecA1Pが 求まります。
- A1を始点とする為に足せば、点Pの絶対位置が求まります。この交点は、線分Aと線分Bの交点ではなくて、 直線Aと直線Bの交点になります。
この方法の素晴らしいところは、一意の式で交点が求まるという所です。 いわゆる直線の式 Y=b/a*X+c を使って求める方法もあるようですが、X軸もしくはY軸に平行だった 場合などに、0除算にならないような配慮を行う必要がある為、一意の式で求まらない感じになって しまいます。
そんな訳で、V値とS値に対応する HSV三角形内の座標が求まりました。ただし、V値とS値の合計が1を越える 場合は、HSV三角形の外に交点が求まってしまいます。でも、SAIなどのように「HSV四角形」にした場合の 答えとしては正解なのです。「HSV四角形」ではS=1.0でV=0.0〜1.0の範囲を取る事はアリだからです。 「HSV三角形」の場合はこれはナシなので、RGBからHSVに変換する場合には、VとSの合計が1.0を越えない ように変換する必要があります。
4.5. カラーサークルを描く
表示用のカラーサークル描画を行います。
矩形の描画バッファのピクセル位置を順に走査していき、その座標に対して「点位置から色相に変換する」 で行った色相変換を行います。この時、矩形バッファの中央が(0,0)の中心となる様に考えれば 特に問題は無いと思います。環状になるようにするには、中心からの半径がある範囲に入っている場合 だけ色変換を行い、範囲外の時には適当な背景色で描画します。
描画バッファでの色表現はRGBなので、色相をRGB変換する必要があります。 変換式は「HSV色空間」のWikipedia にあるような感じです。Wikipediaでは色相を0〜360°で扱ってますが、この覚え書きでは、 -180°〜+180°で扱っている違いがあります。
4.6. HSV三角形を描く
表示用のHSV三角形描画を行います。
三角形全体を含む矩形領域をピクセル単位で順に走査していき、各ピクセル座標に対して、 三角形内の場合に「点位置から明度/彩度に変換する」と同様に明度と彩度を求めます。 三角形外の場合は適当な背景色で描画します。
カラーサークル描画と同様に、HSV値をRGB変換する必要があります。 色相はカラーサークル描画で求めた感じで求めるとして、明度と彩度を考慮した色変換は、 「点位置から明度/彩度に変換する」の面積比をそのまま色の混合比として使用しました。
pix色 = ((Hue色 * H面積) + (白 * S面積)) / HSV三角形面積
ここでは V値って無くても良いんですよね。
4.7. もう一手間
もうひと手間。HSV三角形内をドラッグするとき、三角形の辺や頂点に乗るポイントを 指定するのは解像度的にかなり難しいです。そこで、三角形の外にドラッグポイントが移動した 時は、その位置に最も近い HSV三角形の辺にポイントがスナップすると、辺や頂点上の 値を楽にポイントする事ができます。
HSV三角形外に点Pがあった場合に、最も点Pに近い三角形辺上の点Xを次のような感じ で求めてみました。
- 三つの辺それぞれに対して、点Pに最も近い 辺上の点X1,X2,X3を求める。
- 点Pと各辺上の点X1,X2,X3の距離が最も近いものを、最終的な点Xとして選択する。
- 点Xで決定した場合はその点でHSVの混合比を求める。
直線Aと点Pが最も接近する直線A上の点Xは内積を利用して求めました。
点X = 正規化したvecA1A2 * ((vecA1P・vecA1A2) / vecA1A2の長さ) + A1 (※「・」は内積を示す)
作図すると以下のような感じ。
「((vecA1P・vecA1A2) / vecA1A2の長さ)」は向きも含めた vecA1Pの長さとなっています。 これと「vecA1A2の長さ」との比が 0以上かつ1.0以下 の場合に線分内に収まっていると 判断できます。 範囲を超える場合はA1もしくはA2にスナップしたいですが、比が1.0より大きい場合はX=A2に、 比が0より小さい場合はX=A1とすれば、スナップした事になります。
5. 色々あって完成
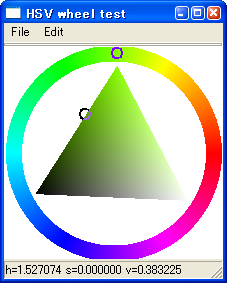
これまでの要素を含めてコーディングして完成。
とにかく面倒臭くなってしまった元凶は、明度/彩度指定に三角形方式を選んだ事に尽きると思います。 また、色の指定にHSVホイールのみを使うのであれば、値の決定自体はそんなに難しい所 ではなかったように思うのですが、HSV値からカラーサークル内、HSV三角形の位置を逆変換 しなくてはならない点が、特に面倒臭いところだったように思います。 さり気に結構重い処理だったりするので、一昔前のPCだとかなりモッサリした動きになるんじゃ ないかと思います。
で、こんだけ面倒臭い要素を含めて実現してみたのですが、なんとなく三角形方式は使いにくいわ。 そんな所がへっぽこ風という事で終わり。
6. 履歴
2010/05/23 : 初版 2010/11/09 : 02版 誤記をちょろっと修正 2012/03/22 : ページをEmacsのorg-modeを使用して生成してみた。内容は2010/11/09と同じです。 2012/04/17 : 「4.7もう一手間」で点Xの位置を求める式が間違えていたのを修正。 2012/04/28 : 「4.7もう一手間」で線分の内に入っているかの判定説明が間違えていたのを修正。 2015/05/27 : Cinderellaの図についての留意点を追記。Cinderella2対応版に差し替え。 2022/07/02 : Javaアップレット廃止にともない表示不可となっていた図を CindyJSで表示するように対応。